Unlock a world of possibilities! Login now and discover the exclusive benefits awaiting you.
- Qlik Community
- :
- All Forums
- :
- QlikView App Dev
- :
- better way to get time-weighted average than join ...
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
better way to get time-weighted average than join + peek + groupby?
First off, my current implementation is working. It is just *slow*. I'm doing what Mr. Cronström recommends here: (Generating Missing Data In QlikView). Everything I know, I owe to that!
I have external data with the value I care about (Z) for each product (X) at a time (Y). The times have millisecond-level granularity. There is only an entry in the external data when the value I care about (Z) changes for a given product (X). Thus, there are many missing values.
My goal is to arrive at the time-weighted average value Z for each product X with whole-second level of detail. To briefly illustrate why I want time-weighted average values, consider this example. For a given product X, its Z value from 00:00:00.000 to 00:00:00.025 was 5; its value from 00:00:00.025 to 00:00:01 was 10. For most of that whole second 00:00:00, the value was 10. A naive (simple) average of 7.5 doesn't accurately summarize the "average" state of product X during the whole second 00:00:00.
To get here, I'm taking the cartesian product of milliseconds and unique products. Then, I'm ordering by product and millisecond, and filling in the missing values by PEEKing from above. This gives me an accurate state of the world for every product at every millisecond.
Finally, I'm grouping by whole second and taking the average of Z that I care about. This gets me to an accurate, time-weighted average of Z for each product X over each whole second.
This works, but it is *slow*. My data is at the 25 millisecond granularity. Thus, I have 24 hours * 60 minutes * 60 seconds * (1000/25) possible times. I have ~2000 products. Doing the math, my cartesian product is ~6,912,000,000 values.
My question has three parts:
1) Does it make a difference that one of my dimensions is a numeric (time) value?
2) Is there a faster way to do this than the default method of cartesian product + peek?
3) Since my final goal is time-weighted average, should I even be using the cartesian product + peek?
Thanks!
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
hope I understand
from your example
in the interval from 0 to 1 sec. you only have 2 values
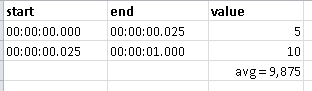
and you can calculate the average using these 2 values (in one sec there is 40 * 25 millisec, etc.....); I think there is no need to generate the other 38 values (one every 25 millisec) to calculate the average at the second level
avg= (5*1 + 10*39) / 40
in this way you can reduce the record from ~6,912,000,000 to ~6,912,000,000 / 20 (assuming you have 2 entry for second)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
hope I understand
from your example
in the interval from 0 to 1 sec. you only have 2 values

and you can calculate the average using these 2 values (in one sec there is 40 * 25 millisec, etc.....); I think there is no need to generate the other 38 values (one every 25 millisec) to calculate the average at the second level
avg= (5*1 + 10*39) / 40
in this way you can reduce the record from ~6,912,000,000 to ~6,912,000,000 / 20 (assuming you have 2 entry for second)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Massimo,
Thank you for the suggestion. Unfortunately, my example above was just to demonstrate the need for a time-weighted average.
My data is "lumpy". Some whole seconds have an update for a single product (X) almost every 25-millisecond bucket. Other times (Y) or products (X), I don't have a value at all for entire seconds. In that case, the value is inherited from the last valid value by way of the PEEK function.
Thanks.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Massimo,
I haven't forgotten this suggestion, and I've been chewing on it. I'm going to try to build on your suggestion by calculating for each line what the count of "missing" ticks was, then using that to weight my values. It's trying to back into the missing values without having to generate the Cartesian product and fill them in.
Sadly, doing an A/B test between the two methods may take a while. Ultimately, I'll follow-up here with an update.
Thanks!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Massimo,
I finally had some time to pursue this. Your suggestion pointed me in the right direction. Counting the "missing" times was a great way to fill in the gaps.
The only wrinkle was that I first had to fill in just the missing, "important" times and peek from the prior row with valid data. In this case, I made sure to have a record for every fifth second. This allowed me to have accurate time-weighted average values, but still have meaningful summary values for every five seconds.
Thank you VERY much for your pointer!