Unlock a world of possibilities! Login now and discover the exclusive benefits awaiting you.
- Qlik Community
- :
- All Forums
- :
- QlikView App Dev
- :
- Rounding differences between QV 11 & 12
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Rounding differences between QV 11 & 12
Has anyone noticed that rounding is performing differently in QV11.20 vs QV12.10?
=NUM(102.06500, '#.00') & =num(102.07500, '#.00')
| QV version | 102.06500 | 102.07500 |
|---|---|---|
| QV11.20 SR9 | 102.07 | 102.07 |
| QV12.10 SR3 | 102.06 | 102.08 |
Is this a bug or a design difference?
John
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
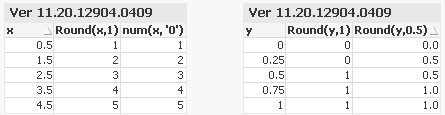
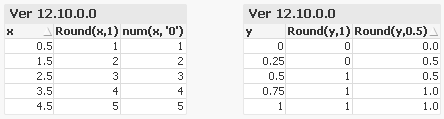
There is a design difference. Or rather, it is a bug-fix. There was a bug that caused a small unnecessary internal rounding, and that resulted in some corner cases being incorrectly rounded. But it was really only visible in cases where you wanted a tie-breaking, e.g.: Should 0.65 be rounded upwards to 0.7 or downwards to 0.6? So the version 12 behaviour should be more correct.
Note also that 102.065 cannot be exactly represented internally - it has no exact binary representation. Hence, it is really not a tie-breaking issue. The number is always below or above the cutoff limit. See Rounding Errors.
If you want to test how the QIX engine handles real tie-breaks, you need to use exact binary numbers. Then you will find that it always rounds upwards, and that it hasn't changed between v11.2 and v12.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Maybe hic can help?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
There is a design difference. Or rather, it is a bug-fix. There was a bug that caused a small unnecessary internal rounding, and that resulted in some corner cases being incorrectly rounded. But it was really only visible in cases where you wanted a tie-breaking, e.g.: Should 0.65 be rounded upwards to 0.7 or downwards to 0.6? So the version 12 behaviour should be more correct.
Note also that 102.065 cannot be exactly represented internally - it has no exact binary representation. Hence, it is really not a tie-breaking issue. The number is always below or above the cutoff limit. See Rounding Errors.
If you want to test how the QIX engine handles real tie-breaks, you need to use exact binary numbers. Then you will find that it always rounds upwards, and that it hasn't changed between v11.2 and v12.

