Unlock a world of possibilities! Login now and discover the exclusive benefits awaiting you.
- Subscribe to RSS Feed
- Mark as New
- Mark as Read
- Bookmark
- Subscribe
- Printer Friendly Page
- Report Inappropriate Content
All sets are not equal. Some sets are indeed more fundamental than others.
Apart from the two trivial sets {0} (nothing) and {1} (everything), the most fundamental group of sets are the Natural Sets. These are the sets that can be defined as a selection or through a Set modifier, e.g.
{$}
{$<Country={France}>}
{BM01<Product=>}
Compare these to the non-natural sets, where set operators are used for the set definitions:
{1-$}
{BM01*$}
To understand the difference between the two, you need to know the difference between element sets (lists of distinct field values) and record sets (lists of records in the internal database). See Why is it called Set Analysis?.
Internally, all sets are stored as element sets and/or record sets in state vectors. For Natural sets both the element sets and the record set can be stored, but for the non-natural sets only the record set can be stored. The reason is that there are no well-defined element sets for non-natural sets.
Consider for instance the following table where you want to sum numbers that are not assigned to a customer:
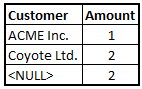
With Set analysis, this is straightforward. The second expression calculates exactly this, using a non-natural set:
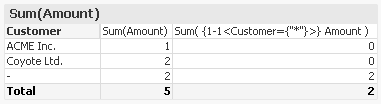
But if you try to create the same filter using a selection in the list boxes, you will find that it is not possible - Null is not selectable.
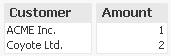
No matter how you select from the two list boxes, you cannot recreate this filter. Hence, a non-natural set cannot always be defined through a selection, and thus cannot be stored as element sets.
From a logical perspective, you could say that Natural sets are always defined by the element sets (the state vectors of the symbol tables), while the record set (the state vector of the data table) is just the result of the logical inference. For non-natural sets, it is the other way around: These are defined by the record set.
This has a number of consequences. First, it is not possible to use a set expression like
{ (BM01 * BM02) <Field={x,y}> }
where the normal (round) brackets imply that the intersection between BM01 and BM02 should be evaluated before the set modifier is applied. The reason is of course that there is no element set that can be modified.
Further, you cannot use non-natural sets inside the P() and E() functions. The reason is that these functions return an element set, but it is not possible to deduce that from the record set of a non-natural set.
Finally, a measure cannot always be attributed to the right dimensional value if a non-natural set is used. For example, in the chart below, you can see that some excluded sales numbers are attributed to the correct ProductCategories, whereas others have NULL as ProductCategory.
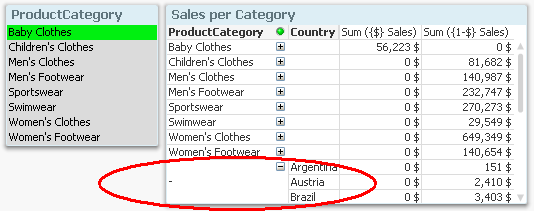
Whether the assignment is correctly made or not, depends on the data model. In this specific case, the number cannot be assigned if it pertains to a country that is excluded by the selection.
Summary:
- Only natural sets can be re-created as interactive selections and stored in bookmarks
- Only natural sets can be modified
- Only natural sets can be used inside the P() and E() functions
- A measure cannot always be attributed to the correct dimensional value if a non-natural set is used
Further reading related to this topic:
Why is it called Set Analysis?
You must be a registered user to add a comment. If you've already registered, sign in. Otherwise, register and sign in.