Unlock a world of possibilities! Login now and discover the exclusive benefits awaiting you.
Featured Content
-
Qlik Cloud Error: 401 Authorization Required after removal of deprecated Develop...
Updated 4th of February, 2026: the role and keys toggle has been removed as announced. The following two items were deprecated in June 2025 and remove... Show MoreUpdated 4th of February, 2026: the role and keys toggle has been removed as announced.
The following two items were deprecated in June 2025 and removed in February 2026:
- Developer role
- Enable API keys toggle
This can lead to Error: 401 Authorization Required when executing third party API calls.
What actions do I need to take?To replace the deprecated built-in role, migrate your users away from the Developer role to a Custom Role with the required permissions (Manage API Keys).
To create and assign a replacement custom role:
- In the Administration activity center, go to Manage users
- On the Permissions tab, select Create new
- Name the new custom role using your organization's naming convention.
For example: "AllowManageAPIKeys" - Expand Features and Actions
- Then expand Developer
- Set Manage API keys to Allowed and press 'confirm' to complete the creation of the new custom role
- In the same screen, click the dropdown menu on the right side of the screen.
- Use the Assign button feature to find and assign the new custom role to specific users or groups. Do so specifically for those who previously had the now deprecated Developer role
- Remove the deprecated role from those users or groups
For additional reading on the Managed API Keys (set to Not allowed by default), see Permissions in User Default and custom roles | Permission settings — Features and actions.
When were the deprecated items removed?
The Developer role and Enable API keys toggle were removed in February 2026.
What will happen if we fail to migrate?
Once the Developer role has been removed, users who have not been updated to use the “Manage API keys” = Allow permission will:
- Be unable to access the API keys UI in Profile > Settings
- Find their API keys disabled, resulting in 3rd-party integrations failing (Error: 401 Authorization Required)
API keys are not deleted from Qlik Cloud and will automatically be re-enabled once a user has been assigned the required Manage API Keys permissions.
To resolve this, a Tenant Administrator needs to act as outlined in What action do I need to take?
How was the deprecation communicated and what products were affected by the removal of the role and toggle?
The deprecation notice was communicated in an Administration announcement and documented on our What's New in Qlik Cloud feed. See Developer role and API key toggle deprecated | 6/16/2025 for details.
The following products were affacted:
- Qlik Cloud Analytics
- Qlik Talend Cloud
Related Information
-
How to contact Qlik Support
Qlik offers a wide range of channels to assist you in troubleshooting, answering frequently asked questions, and getting in touch with our technical e... Show MoreQlik offers a wide range of channels to assist you in troubleshooting, answering frequently asked questions, and getting in touch with our technical experts. In this article, we guide you through all available avenues to secure your best possible experience.
For details on our terms and conditions, review the Qlik Support Policy.
Index:
- Support and Professional Services; who to contact when.
- Qlik Support: How to access the support you need
- 1. Qlik Community, Forums & Knowledge Base
- The Knowledge Base
- Blogs
- Our Support programs:
- The Qlik Forums
- Ideation
- How to create a Qlik ID
- 2. Chat
- 3. Qlik Support Case Portal
- Escalate a Support Case
- Phone Numbers
- Resources
Support and Professional Services; who to contact when.
We're happy to help! Here's a breakdown of resources for each type of need.
Support Professional Services (*) Reactively fixes technical issues as well as answers narrowly defined specific questions. Handles administrative issues to keep the product up-to-date and functioning. Proactively accelerates projects, reduces risk, and achieves optimal configurations. Delivers expert help for training, planning, implementation, and performance improvement. - Error messages
- Task crashes
- Latency issues (due to errors or 1-1 mode)
- Performance degradation without config changes
- Specific questions
- Licensing requests
- Bug Report / Hotfixes
- Not functioning as designed or documented
- Software regression
- Deployment Implementation
- Setting up new endpoints
- Performance Tuning
- Architecture design or optimization
- Automation
- Customization
- Environment Migration
- Health Check
- New functionality walkthrough
- Realtime upgrade assistance
(*) reach out to your Account Manager or Customer Success Manager
Qlik Support: How to access the support you need
1. Qlik Community, Forums & Knowledge Base
Your first line of support: https://community.qlik.com/
Looking for content? Type your question into our global search bar:
The Knowledge Base
Leverage the enhanced and continuously updated Knowledge Base to find solutions to your questions and best practice guides. Bookmark this page for quick access!
- Go to the Official Support Articles Knowledge base
- Type your question into our Search Engine
- Need more filters?
- Filter by Product
- Or switch tabs to browse content in the global community, on our Help Site, or even on our Youtube channel
Blogs
Subscribe to maximize your Qlik experience!
The Support Updates Blog
The Support Updates blog delivers important and useful Qlik Support information about end-of-product support, new service releases, and general support topics. (click)The Qlik Design Blog
The Design blog is all about product and Qlik solutions, such as scripting, data modelling, visual design, extensions, best practices, and more! (click)The Product Innovation Blog
By reading the Product Innovation blog, you will learn about what's new across all of the products in our growing Qlik product portfolio. (click)Our Support programs:
Q&A with Qlik
Live sessions with Qlik Experts in which we focus on your questions.Techspert Talks
Techspert Talks is a free webinar to facilitate knowledge sharing held on a monthly basis.Technical Adoption Workshops
Our in depth, hands-on workshops allow new Qlik Cloud Admins to build alongside Qlik Experts.Qlik Fix
Qlik Fix is a series of short video with helpful solutions for Qlik customers and partners.The Qlik Forums
- Quick, convenient, 24/7 availability
- Monitored by Qlik Experts
- New releases publicly announced within Qlik Community forums (click)
- Local language groups available (click)
Ideation
Suggest an idea, and influence the next generation of Qlik features!
Search & Submit Ideas
Ideation GuidelinesHow to create a Qlik ID
Get the full value of the community.
Register a Qlik ID:
- Go to register.myqlik.qlik.com
If you already have an account, please see How To Reset The Password of a Qlik Account for help using your existing account. - You must enter your company name exactly as it appears on your license or there will be significant delays in getting access.
- You will receive a system-generated email with an activation link for your new account. NOTE, this link will expire after 24 hours.
If you need additional details, see: Additional guidance on registering for a Qlik account
If you encounter problems with your Qlik ID, contact us through Live Chat!
2. Chat
Incidents are supported through our Chat, by clicking Chat Now on any Support Page across Qlik Community.
To raise a new issue, all you need to do is chat with us. With this, we can:
- Answer common questions instantly through our chatbot
- Have a live agent troubleshoot in real time
- With items that will take further investigating, we will create a case on your behalf with step-by-step intake questions.
3. Qlik Support Case Portal
Log in to manage and track your active cases in the Case Portal. (click)
Before you can access the Support Portal, please complete your Community account setup. See First time access to the Qlik Customer Support Portal fails with: Unauthorized Access Please try signing out and sign in again.
Please note: to create a new case, it is easiest to do so via our chat (see above). Our chat will log your case through a series of guided intake questions.
Your advantages:
- Self-service access to all incidents so that you can track progress
- Option to upload documentation and troubleshooting files
- Option to include additional stakeholders and watchers to view active cases
- Follow-up conversations
When creating a case, you will be prompted to enter problem type and issue level. Definitions shared below:
Problem Type
Select Account Related for issues with your account, licenses, downloads, or payment.
Select Product Related for technical issues with Qlik products and platforms.
Priority
If your issue is account related, you will be asked to select a Priority level:
Select Medium/Low if the system is accessible, but there are some functional limitations that are not critical in the daily operation.
Select High if there are significant impacts on normal work or performance.
Select Urgent if there are major impacts on business-critical work or performance.
Severity
If your issue is product related, you will be asked to select a Severity level:
Severity 1: Qlik production software is down or not available, but not because of scheduled maintenance and/or upgrades.
Severity 2: Major functionality is not working in accordance with the technical specifications in documentation or significant performance degradation is experienced so that critical business operations cannot be performed.
Severity 3: Any error that is not Severity 1 Error or Severity 2 Issue. For more information, visit our Qlik Support Policy.
Escalate a Support Case
If you require a support case escalation, you have two options:
- Request to escalate within the case, mentioning the business reasons.
To escalate a support incident successfully, mention your intention to escalate in the open support case. This will begin the escalation process. - Contact your Regional Support Manager
If more attention is required, contact your regional support manager. You can find a full list of regional support managers in the How to escalate a support case article.
Phone Numbers
When other Support Channels are down for maintenance, please contact us via phone for high severity production-down concerns.
- Qlik Data Analytics: 1-877-754-5843
- Qlik Data Integration: 1-781-730-4060
- Talend AMER Region: 1-800-810-3065
- Talend UK Region: 44-800-098-8473
- Talend APAC Region: 65-800-492-2269
Resources
A collection of useful links.
Qlik Cloud Status Page
Keep up to date with Qlik Cloud's status.
Support Policy
Review our Service Level Agreements and License Agreements.
Live Chat and Case Portal
Your one stop to contact us.
Recent Documents
-
Qlik Automate: How to run an automation between working hours and only on busine...
This article documents how to schedule automations between specific hours and days of the week. This is intended as a workaround until a native soluti... Show MoreThis article documents how to schedule automations between specific hours and days of the week. This is intended as a workaround until a native solution is delivered.
Getting started
- Download the attached automation file (Automation on business hours and working days only.json) and import it into a blank automation workspace. See How to import and export automations.
- Configure the timezone in the first variable block.
- Update the first condition block to set the latest time (hour) and day of the week for which you want the automation to run. Define the hour in the 24-hour format and the day in a 1 (Monday) to 7 (Sunday) format.
For example, 5 pm on a Friday would be 17 (hour) and 5 (day). - Configure the Schedule Start and Time Interval parameters on the first Update Automation Schedule block. For Schedule Start you should only edit the time parameter, no changes are required to the date formula.
- Update the second condition block to set the earliest and latest time (hour) at which you want the automation to run on business days.
Define the hour in the 24-hour format.
For example, 5 pm would be 17. - Now configure the other Update Automation Schedule blocks similarly to step 4, but do not edit the Schedule Start parameter on the middle Update Automation Schedule block as this will follow the automation's scheduled interval.
The information in this article is provided as-is and will be used at your discretion. Depending on the tool(s) used, customization(s), and/or other factors, ongoing support on the solution below may not be provided by Qlik Support.
Environment
- Qlik Cloud
- Qlik Application Automation
-
Qlik Replicate and Qlik Enterprise Manager Full Load Only task: Reloading multip...
In a Full Load Only task, clicking Reload will reload all tables by default. If you want to reload only specific tables, follow these steps: Open the... Show MoreIn a Full Load Only task, clicking Reload will reload all tables by default. If you want to reload only specific tables, follow these steps:
- Open the Qlik Replicate Console or Qlik Enterprise Manager Console and navigate to the Monitor page for your task
- Stop the task if it is running
- Under the Full Load section, you will see the tables that were previously loaded
- Press and hold the CTRL key, then click to select the tables (A) you want to reload; once selected, click Reload (B)
- The selected tables will appear in the Queued state
- From the Run option menu (A), choose Resume Processing… (B)
- The corresponding tables will then be reloaded.
For an alternative method, see Qlik Enterprise Manager Full Load Only task: How to reload specific tables in a Full Load Only task via REST API.
Environment
- Qlik Replicate: All versions
- Qlik Enterprise Manager: All versions
-
Qlik Enterprise Manager Full Load Only task: How to reload specific tables in a ...
By default, clicking Reload in a Full Load Only task reloads all tables. If you want to reload only specific tables, you can use the REST API. The exa... Show MoreBy default, clicking Reload in a Full Load Only task reloads all tables. If you want to reload only specific tables, you can use the REST API. The examples in this article use curl.
Test Environment (example values)
- Hostname:
qem.qlik.com - Server name:
LocalQR(defined for the Qlik Replicate server) - Task name:
Full_Load_Only - Tables:
dbo.test01, dbo.test02
Replace these values with your own environment details.
Steps:
- Stop the task
Make sure the task is in a Stopped state before reloading tables. - Get the API Session ID:
curl -i -k -u --header "Authorization: Basic cWFAcWE6cWE=" https://qem.qlik.com/attunityenterprisemanager/api/V1/login
A successful response includes the session ID in the header:EnterpriseManager.APISessionID: lfohcqKvZzNdc33_r7NHCw - Save this value for subsequent requests
- Queue a specific table for reload
Use the session ID to add a table (e.g., test01) to the reload queue.This step only queues the table. It does not start the reload yet.
curl -i -k -X POST ^--header "EnterpriseManager.APISessionID: lfohcqKvZzNdc33_r7NHCw" ^--header "Content-Length: 0""https://qem.qlik.com/attunityenterprisemanager/api/V1/servers/LocalQR/tasks/Full_Load_Only/tables?action=reload&schema=dbo&table=test01" - Queue additional tables
Repeat step 4 for each additional table (such as test02) you want to add to the reload queue.curl -i -k -X POST ^--header "EnterpriseManager.APISessionID: lfohcqKvZzNdc33_r7NHCw" ^--header "Content-Length: 0""https://qem.qlik.com/attunityenterprisemanager/api/V1/servers/LocalQR/tasks/Full_Load_Only/tables?action=reload&schema=dbo&table=test02" - Resume the task to start reloading
Once all desired tables are queued, resume the task. At this point, the reload process for those tables will actually begin.curl -i -k -X POST ^--header "EnterpriseManager.APISessionID: lfohcqKvZzNdc33_r7NHCw" ^--header "Content-Length: 0""https://qem.qlik.com/attunityenterprisemanager/api/V1/servers/LocalQR/tasks/Full_Load_Only?action=run&option=RESUME_PROCESSING"
For an alternative method, see Qlik Replicate and Qlik Enterprise Manager Full Load Only task: Reloading multiple selected tables using the web console.
Environment
- Qlik Enterprise Manager: All versions
- Hostname:
-
Qlik Sense Insight Advisor ignores Alternate States
Insight Advisor does not filter data when a sheet is using Alternate States. Instead, it operates exclusively in the default state. This is working a... Show MoreInsight Advisor does not filter data when a sheet is using Alternate States. Instead, it operates exclusively in the default state.
This is working as expected.
As of January 2026, Insight Advisor is no longer actively in development. Look into Qlik Answers for a feature-rich replacement (available on Qlik Cloud).
Environment
- Qlik Insight Advisor
- Qlik Cloud
- Qlik Sense Enterprise on Windows
-
Qlik Cloud Error: 401 Authorization Required after removal of deprecated Develop...
Updated 4th of February, 2026: the role and keys toggle has been removed as announced. The following two items were deprecated in June 2025 and remove... Show MoreUpdated 4th of February, 2026: the role and keys toggle has been removed as announced.
The following two items were deprecated in June 2025 and removed in February 2026:
- Developer role
- Enable API keys toggle
This can lead to Error: 401 Authorization Required when executing third party API calls.
What actions do I need to take?To replace the deprecated built-in role, migrate your users away from the Developer role to a Custom Role with the required permissions (Manage API Keys).
To create and assign a replacement custom role:
- In the Administration activity center, go to Manage users
- On the Permissions tab, select Create new
- Name the new custom role using your organization's naming convention.
For example: "AllowManageAPIKeys" - Expand Features and Actions
- Then expand Developer
- Set Manage API keys to Allowed and press 'confirm' to complete the creation of the new custom role
- In the same screen, click the dropdown menu on the right side of the screen.
- Use the Assign button feature to find and assign the new custom role to specific users or groups. Do so specifically for those who previously had the now deprecated Developer role
- Remove the deprecated role from those users or groups
For additional reading on the Managed API Keys (set to Not allowed by default), see Permissions in User Default and custom roles | Permission settings — Features and actions.
When were the deprecated items removed?
The Developer role and Enable API keys toggle were removed in February 2026.
What will happen if we fail to migrate?
Once the Developer role has been removed, users who have not been updated to use the “Manage API keys” = Allow permission will:
- Be unable to access the API keys UI in Profile > Settings
- Find their API keys disabled, resulting in 3rd-party integrations failing (Error: 401 Authorization Required)
API keys are not deleted from Qlik Cloud and will automatically be re-enabled once a user has been assigned the required Manage API Keys permissions.
To resolve this, a Tenant Administrator needs to act as outlined in What action do I need to take?
How was the deprecation communicated and what products were affected by the removal of the role and toggle?
The deprecation notice was communicated in an Administration announcement and documented on our What's New in Qlik Cloud feed. See Developer role and API key toggle deprecated | 6/16/2025 for details.
The following products were affacted:
- Qlik Cloud Analytics
- Qlik Talend Cloud
Related Information
-
Is the Qlik Sense Analytics Snowflake ODBC connector developed by Qlik?
The ODBC connector used by Qlik Analytics for Snowflake is developed by Snowflake and integrated into Qlik. Performance and stability are on par with ... Show MoreThe ODBC connector used by Qlik Analytics for Snowflake is developed by Snowflake and integrated into Qlik. Performance and stability are on par with the Snowflake ODBC connector itself.
Environment
- Qlik Cloud Analytics
- Qlik Sense Enterprise on Windows
- Qlik ODBC Connector Package
-
Qlik Sense WebSocket Connectivity Tester
Qlik Sense uses HTTP, HTTPS, and WebSockets to transfer information to and from Qlik Sense. The attached Webscoket Connectivity tester can be used to... Show MoreQlik Sense uses HTTP, HTTPS, and WebSockets to transfer information to and from Qlik Sense.
The attached Webscoket Connectivity tester can be used to verify protocol compliance, indicating if a network policy, firewall, or other perimeter device is blocking any of the required connections.
If the tests return as unsuccessful, please engage your network team.
The QlikSenseWEbsocketConnectivtyTester is not an officially supported application and is provided as is. It is intended to assist in troubleshooting, but further investigation of an unsuccessful test will require your network team's involvement. To run this tool, the Qlik Sense server must have a working internet connection.
Environment:
Qlik Sense Enterprise on Windows
For Qlik Sense Enterprise on Windows November 2024 and later:
Since the introduction of extended WebSocket CSRF protection, using the WebSocket Connectivity tester on any version later than November 2024 requires a temporary configuration change.
- Open the Proxy.exe.config stored in C:\Program Files\Qlik\Sense\Proxy\
- Locate
<add key="WebSocketCSWSHCheckEnabled" value="true"/>
- Change it to
<add key="WebSocketCSWSHCheckEnabled" value="false"/>
- Restart the proxy
- Run the WebSocket Connectivity tester
- Revert the change
How to use the Websocket Connectivity Tester
- Download the attached package or download the package from GitHub: https://github.com/flautrup/QlikSenseWebsocketConnectivityTester
- Unzip the file
- Login to the Qlik Sense Management Console
- Create a Content Library
- Go to Content libraries
- Click and Create New
- Name the Content Library: WebSocketTester
- Verify and modify the Security Rule
Note that in our example, any user is allowed to access this WebSocketTester. - Click Apply
- Click Contents in the Associated items menu
- Click Upload
- Upload the QlikSenseWebsocketTest.html file.
- Copy the correct URL from the URL path
- Open a web browser (from any machine from which you wish to test the WebSocket connection).
- Paste the URL path and prefix the fully qualified domain name and https.
Example: https://qlikserver3.domain.local/content/WebSocketTester/QlikSenseWebsocketTest.html
What to do if any of them fail?
Verify that WebSocket is enabled in the network infrastructure, such as firewalls, browsers, reverse proxies, etc.
See the article below under Related Content for additional steps.
Related Content
-
Qlik Replicate: SAP ExtractorTask unloading the extractor data from SAP from a p...
If a Qlik Replicate task with a SAP Extractor endpoint as a source does not stop cleanly (or fails), the SAP Extractor background job may continue to ... Show MoreIf a Qlik Replicate task with a SAP Extractor endpoint as a source does not stop cleanly (or fails), the SAP Extractor background job may continue to run in SAP.
This will cause duplicated data to be read from SAP, as the existing SAP job does not stop if the Qlik Replicate task fails or fails to stop cleanly.
Resolution
Qlik Replicate 2025.11 SP03 introduced a new Internal Parameter to resolve this.
- Go to the SAP endpoint connection
- Switch to the Advanced tab
- Click Internal Parameters
- Enter the parameter removeJobAfterTaskStop
- Set the removeJobAfterTaskStop to true
- Save the endpoint
- Stop and resume any task using the endpoint; this will make sure the changes take effect
Internal Investigation ID(s)
SUPPORT-6807
Environment
- Qlik Replicate
-
Qlik Replicate: ORA-00932 inconsistent datatypes: expected NCLOB got CHAR
PostgreSQL Source tables with a Character Varying (8000) datatype would be created as a Varchar(255) datatype on the Oracle Target tables as the defau... Show MorePostgreSQL Source tables with a Character Varying (8000) datatype would be created as a Varchar(255) datatype on the Oracle Target tables as the default.
This error will occur with the default settings, as Oracle only supports up to 255 characters for the datatype. Incoming records with a character count higher than 255 are treated as a CLOB datatype and cannot fit in all of the incoming 8000 bytes/char of data.
The following error is written to the log:
[TARGET_APPLY ]T: ORA-00932: inconsistent datatypes: expected NCLOB got CHAR [1020436] (oracle_endpoint_bulk.c:812)
Environment
- Qlik Replicate any version
- PostgreSQL Source
- Oracle Target
Resolution
Adjust the datatype in the Qlik Replicate task table settings to transform the character varying (8000) datatypes to a CLOB datatype.
This will create CLOB columns on the target and allow the large incoming records to fit in the target table.
Note that the transformation will need a target table reload to rebuild the table with a new datatype.
Cause
Default task settings create the column with a varchar(255) datatype, while it needs to be a CLOB datatype, as any size over 255 will not fit in the target table if an incoming record exceeds 255 characters in size.
-
Qlik Cloud Monitoring Apps Workflow Guide
This template was updated on December 4th, 2025 to replace the original installer and API key rotator with a new, unified deployer automation. Please... Show MoreThis template was updated on December 4th, 2025 to replace the original installer and API key rotator with a new, unified deployer automation. Please disable or delete any existing installers, and create a new automation, picking the Qlik Cloud monitoring app deployer template from the App installers category.
Installing, upgrading, and managing the Qlik Cloud Monitoring Apps has just gotten a whole lot easier! With a single Qlik Automate template, you can now install and update the apps on a schedule with a set-and-forget installer using an out-of-the-box Qlik Automate template. It can also handle API key rotation required for the data connection, ensuring the data connection is always operational.
Some monitoring apps are designed for specific Qlik Cloud subscription types. Refer to the compatibility matrix within the Qlik Cloud Monitoring Apps repository.
'Qlik Cloud Monitoring Apps deployer' template overview
This automation template is a set-and-forget template for managing the Qlik Cloud Monitoring Applications, including but not limited to the App Analyzer, Entitlement Analyzer, Reload Analyzer, and Access Evaluator applications. Leverage this automation template to quickly and easily install and update these or a subset of these applications with all their dependencies. The applications themselves are community-supported; and, they are provided through Qlik's Open-Source Software (OSS) GitHub and thus are subject to Qlik's open-source guidelines and policies.
For more information, refer to the GitHub repository.
Features
- Can install/upgrade all or select apps.
- Can create or leverage existing spaces.
- Programmatically verified prerequisite settings, roles, and entitlements, notifying the user during the process if changes in configuration are required, and why.
- Installs latest versions of specified applications from Qlik’s OSS GitHub.
- Creates required API key.
- Creates required analytics data connection.
- Creates a daily reload schedule.
- Reload applications post-install.
- Tags apps appropriately to track which are installed and their respective versions.
- Supports both user and capacity-based subscriptions.
Configuration:
Update just the configuration area to define how the automation runs, then test run, and set it on a weekly or monthly schedule as desired.
Configure the run mode of the template using 7 variable blocks
Users should review the following variables:
- configuredMonitoringApps: contains the list of the monitoring applications which will be installed and maintained. Delete any applications not required before running (default: all apps listed).
- refreshConnectorCredentials: determines whether the monitoring application REST connection and associated API key will be regenerated every run (default: true).
- reloadNow: determines whether apps are reloaded immediately following updates (default: true).
- reloadScheduleHour: determines at which hour of the day the apps reload at for the daily schedule in UTC timezone (default: 06)
- sharedSpaceName: defines the name of the shared space used to import the apps into prior to publishing. If the space doesn't exist, it'll be created. If the space exists, the user will be added to it with the required permissions (default: Monitoring - staging).
- managedSpaceName: defines the name of the managed space the apps are published into for consumption/ alerts/ subscription use.If the space doesn't exist, it'll be created. If the space exists, the user will be added to it with the required permissions (default: Monitoring).
- versionsToKeep: determines how many versions of each staged app is kept in the shared space. If set to 0, apps are deleted after publishing. If a positive integer value other than 0, that many apps will be kept for each monitoring app deployed (default: 0).
App management:
If the monitoring applications have been installed manually (i.e., not through this automation), then they will not be detected as existing. The automation will install new copies side-by-side. Any subsequent executions of the automation will detect the newly installed monitoring applications and check their versions, etc. This is due to the fact that the applications are tagged with "QCMA - {appName}" and "QCMA - {version}" during the installation process through the automation. Manually installed applications will not have these tags and therefore will not be detected.
FAQ
Q: Can I re-run the installer to check if any of the monitoring applications are able to be upgraded to a later version?
A: Yes. The automation will update any managed apps that don't match the repository's manifest version.
Q: What if multiple people install monitoring applications in different spaces?
A: The template scopes the application's installation process to a managed space. It will scope the API key name to `QCMA – {spaceId}` of that managed space. This allows the template to install/update the monitoring applications across spaces and across users. If one user installs an application to “Space A” and then another user installs a different monitoring application to “Space A”, the template will see that a data connection and associated API key (in this case from another user) exists for that space already. It will install the application leveraging those pre-existing assets.
Q: What if a new monitoring application is released? Will the template provide the ability to install that application as well?
A: Yes, but an update of the template from the template picker will be required, since the applications are hard coded into the template. The automation will begin to fail with a notification an update is needed once a new version is available.
Q:I have updated my application, but I noticed that it did not preserve the history. Why is that?
A: Each upgrade may generate a new set of QVDs if the data models for the applications have changed due to bug fixes, updates, new features, etc. The history is preserved in the prior versions of the application’s QVDs, so the data is never deleted and can be loaded into the older version.
-
Customizing Qlik Sense Enterprise on Windows Forms Login Page
Ever wanted to brand or customize the default Qlik Sense Login page? The functionality exists, and it's really as simple as just designing your HTML p... Show MoreEver wanted to brand or customize the default Qlik Sense Login page?
The functionality exists, and it's really as simple as just designing your HTML page and 'POSTing' it into your environment.
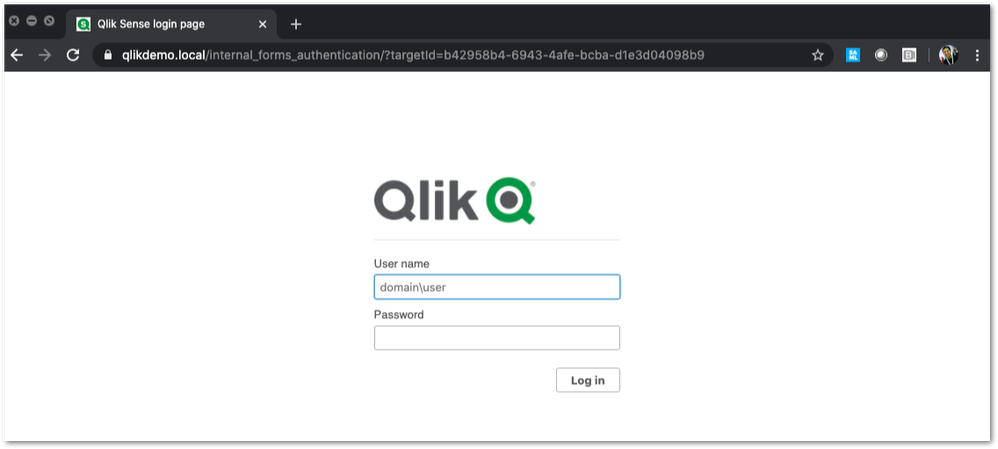
We've all seen the standard Qlik Sense Login page, this article is all about customizing this page.
This customization is provided as is. Qlik Support cannot provide continued support of the solution. For assistance, reach out to our Professional Services or engage in our active Integrations forum.
To customize the page:
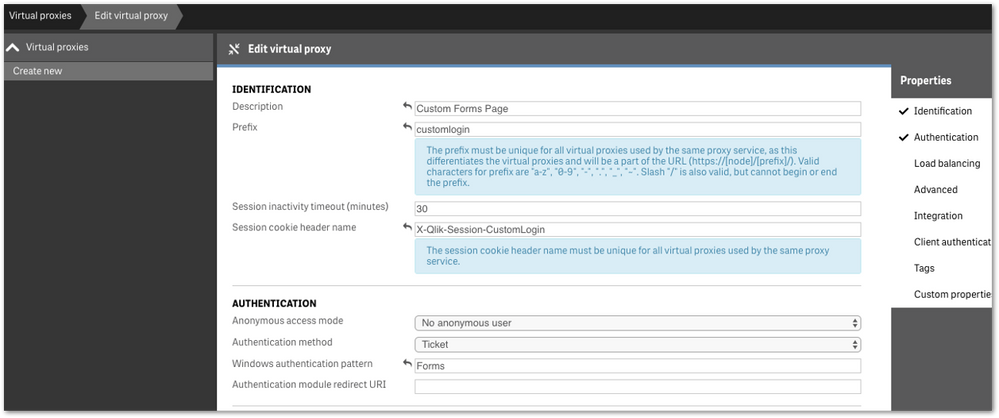
- We highly recommend setting up a new virtual proxy with Forms so you don't impact any users that are using auto-login Windows auth.
Example setup:
Description: Custom Forms Page
Prefix: customlogin
Session cookie header-name: X-Qlik-Session-CustomLogin
Windows authentication pattern: Forms - Once this is done, a good starting point is to download the default login page.
You can open up your web developer tool of choice, go to the login page, and download the HTML response from the GET http://<server>/customlogin/internal_forms_authentication request. It should be roughly a 273 line .html file. - Once you have this file, you can more or less customize it as much as you'd like.
Image files can be inlined as you'll see in the qlik default file, or can be referenced as long as they are publicly accessible. The only thing that needs to exist are the input boxes with appropriate classes and attributes, and the 'Log In' button. - After building out your custom HTML page and it looks great, it needs to be converted to Base64. There are online tools to do this, openssl also has this functionality.
Once you have your Base64 encoded HTML file, then you will want to PUT it into your sense environment. - First, do a GET request on /qrs/proxyservice and find the ID of the proxy service you want this login page to be shown for.
- You will then do a GET request on /qrs/proxyservice/<id> and copy the body of that response. Below is an example of that response.
{ "id": "8817d7ab-e9b2-4816-8332-f8cb869b27c2", "createdDate": "2020-03-23T15:39:33.540Z", "modifiedDate": "2020-05-20T18:46:13.995Z", "modifiedByUserName": "INTERNAL\\sa_api", "customProperties": [], "settings": { "id": "8817d7ab-e9b2-4816-8332-f8cb869b27c2", "createdDate": "2020-03-23T15:39:33.540Z", "modifiedDate": "2020-05-20T18:46:13.995Z", "modifiedByUserName": "INTERNAL\\sa_api", "listenPort": 443, "allowHttp": true, "unencryptedListenPort": 80, "authenticationListenPort": 4244, "kerberosAuthentication": false, "unencryptedAuthenticationListenPort": 4248, "sslBrowserCertificateThumbprint": "e6ee6df78f9afb22db8252cbeb8ad1646fa14142", "keepAliveTimeoutSeconds": 10, "maxHeaderSizeBytes": 16384, "maxHeaderLines": 100, "logVerbosity": { "id": "8817d7ab-e9b2-4816-8332-f8cb869b27c2", "createdDate": "2020-03-23T15:39:33.540Z", "modifiedDate": "2020-05-20T18:46:13.995Z", "modifiedByUserName": "INTERNAL\\sa_api", "logVerbosityAuditActivity": 4, "logVerbosityAuditSecurity": 4, "logVerbosityService": 4, "logVerbosityAudit": 4, "logVerbosityPerformance": 4, "logVerbositySecurity": 4, "logVerbositySystem": 4, "schemaPath": "ProxyService.Settings.LogVerbosity" }, "useWsTrace": false, "performanceLoggingInterval": 5, "restListenPort": 4243, "virtualProxies": [ { "id": "58d03102-656f-4075-a436-056d81144c1f", "prefix": "", "description": "Central Proxy (Default)", "authenticationModuleRedirectUri": "", "sessionModuleBaseUri": "", "loadBalancingModuleBaseUri": "", "useStickyLoadBalancing": false, "loadBalancingServerNodes": [ { "id": "f1d26a45-b0dd-4be1-91d0-34c698e18047", "name": "Central", "hostName": "qlikdemo", "temporaryfilepath": "C:\\Users\\qservice\\AppData\\Local\\Temp\\", "roles": [ { "id": "2a6a0d52-9bb4-4e74-b2b2-b597fa4e4470", "definition": 0, "privileges": null }, { "id": "d2c56b7b-43fd-44ad-a12f-59e778ce575a", "definition": 1, "privileges": null }, { "id": "37244424-96ae-4fe5-9522-088a0e9679e3", "definition": 2, "privileges": null }, { "id": "b770516e-fe8a-43a8-a7a4-318984ee4bd6", "definition": 3, "privileges": null }, { "id": "998b7df8-195f-4382-af18-4e0c023e7f1c", "definition": 4, "privileges": null }, { "id": "2a5325f4-649b-4147-b0b1-f568be1988aa", "definition": 5, "privileges": null } ], "serviceCluster": { "id": "b07fc5f2-f09e-4676-9de6-7d73f637b962", "name": "ServiceCluster", "privileges": null }, "privileges": null } ], "authenticationMethod": 0, "headerAuthenticationMode": 0, "headerAuthenticationHeaderName": "", "headerAuthenticationStaticUserDirectory": "", "headerAuthenticationDynamicUserDirectory": "", "anonymousAccessMode": 0, "windowsAuthenticationEnabledDevicePattern": "Windows", "sessionCookieHeaderName": "X-Qlik-Session", "sessionCookieDomain": "", "additionalResponseHeaders": "", "sessionInactivityTimeout": 30, "extendedSecurityEnvironment": false, "websocketCrossOriginWhiteList": [ "qlikdemo", "qlikdemo.local", "qlikdemo.paris.lan" ], "defaultVirtualProxy": true, "tags": [], "samlMetadataIdP": "", "samlHostUri": "", "samlEntityId": "", "samlAttributeUserId": "", "samlAttributeUserDirectory": "", "samlAttributeSigningAlgorithm": 0, "samlAttributeMap": [], "jwtAttributeUserId": "", "jwtAttributeUserDirectory": "", "jwtAudience": "", "jwtPublicKeyCertificate": "", "jwtAttributeMap": [], "magicLinkHostUri": "", "magicLinkFriendlyName": "", "samlSlo": false, "privileges": null }, { "id": "a8b561ec-f4dc-48a1-8bf1-94772d9aa6cc", "prefix": "header", "description": "header", "authenticationModuleRedirectUri": "", "sessionModuleBaseUri": "", "loadBalancingModuleBaseUri": "", "useStickyLoadBalancing": false, "loadBalancingServerNodes": [ { "id": "f1d26a45-b0dd-4be1-91d0-34c698e18047", "name": "Central", "hostName": "qlikdemo", "temporaryfilepath": "C:\\Users\\qservice\\AppData\\Local\\Temp\\", "roles": [ { "id": "2a6a0d52-9bb4-4e74-b2b2-b597fa4e4470", "definition": 0, "privileges": null }, { "id": "d2c56b7b-43fd-44ad-a12f-59e778ce575a", "definition": 1, "privileges": null }, { "id": "37244424-96ae-4fe5-9522-088a0e9679e3", "definition": 2, "privileges": null }, { "id": "b770516e-fe8a-43a8-a7a4-318984ee4bd6", "definition": 3, "privileges": null }, { "id": "998b7df8-195f-4382-af18-4e0c023e7f1c", "definition": 4, "privileges": null }, { "id": "2a5325f4-649b-4147-b0b1-f568be1988aa", "definition": 5, "privileges": null } ], "serviceCluster": { "id": "b07fc5f2-f09e-4676-9de6-7d73f637b962", "name": "ServiceCluster", "privileges": null }, "privileges": null } ], "authenticationMethod": 1, "headerAuthenticationMode": 1, "headerAuthenticationHeaderName": "userid", "headerAuthenticationStaticUserDirectory": "QLIKDEMO", "headerAuthenticationDynamicUserDirectory": "", "anonymousAccessMode": 0, "windowsAuthenticationEnabledDevicePattern": "Windows", "sessionCookieHeaderName": "X-Qlik-Session-Header", "sessionCookieDomain": "", "additionalResponseHeaders": "", "sessionInactivityTimeout": 30, "extendedSecurityEnvironment": false, "websocketCrossOriginWhiteList": [ "qlikdemo", "qlikdemo.local" ], "defaultVirtualProxy": false, "tags": [], "samlMetadataIdP": "", "samlHostUri": "", "samlEntityId": "", "samlAttributeUserId": "", "samlAttributeUserDirectory": "", "samlAttributeSigningAlgorithm": 0, "samlAttributeMap": [], "jwtAttributeUserId": "", "jwtAttributeUserDirectory": "", "jwtAudience": "", "jwtPublicKeyCertificate": "", "jwtAttributeMap": [], "magicLinkHostUri": "", "magicLinkFriendlyName": "", "samlSlo": false, "privileges": null } ], "formAuthenticationPageTemplate": "", "loggedOutPageTemplate": "", "errorPageTemplate": "", "schemaPath": "ProxyService.Settings" }, "serverNodeConfiguration": { "id": "f1d26a45-b0dd-4be1-91d0-34c698e18047", "name": "Central", "hostName": "qlikdemo", "temporaryfilepath": "C:\\Users\\qservice\\AppData\\Local\\Temp\\", "roles": [ { "id": "2a6a0d52-9bb4-4e74-b2b2-b597fa4e4470", "definition": 0, "privileges": null }, { "id": "d2c56b7b-43fd-44ad-a12f-59e778ce575a", "definition": 1, "privileges": null }, { "id": "37244424-96ae-4fe5-9522-088a0e9679e3", "definition": 2, "privileges": null }, { "id": "b770516e-fe8a-43a8-a7a4-318984ee4bd6", "definition": 3, "privileges": null }, { "id": "998b7df8-195f-4382-af18-4e0c023e7f1c", "definition": 4, "privileges": null }, { "id": "2a5325f4-649b-4147-b0b1-f568be1988aa", "definition": 5, "privileges": null } ], "serviceCluster": { "id": "b07fc5f2-f09e-4676-9de6-7d73f637b962", "name": "ServiceCluster", "privileges": null }, "privileges": null }, "tags": [], "privileges": null, "schemaPath": "ProxyService" } - In the response, locate the formAuthenticationPageTemplate field
- You can then take your base64 encoded HTML file, paste the value into the formAuthenticationPageTemplate field.
Example:
"formAuthenticationPageTemplate": "BASE 64 ENCODED HTML HERE",
Once you have an updated body, you can use the PUT verb (with an updated modifiedDate) to PUT this body back into the repository. Once this is done, you should be able to goto your virtual proxy and you should see your new login page (very Qlik branded in this example):
If your login page does not work and you need to revert back to the default, simply do a GET call on your proxy service, and set formAuthenticationPageTemplate back to an empty string:
formAuthenticationPageTemplate": ""Environment:
- We highly recommend setting up a new virtual proxy with Forms so you don't impact any users that are using auto-login Windows auth.
-
Qlik Write Table FAQ
This document contains frequently asked questions for the Qlik Write Table. Content Data and metadataQ: What happens to changes after 90 days?Q: Whic... Show More -
REST connection fails with error "Timeout when waiting for HTTP response from se...
After loading for a while, Qlik REST connector fails with the following error messages: QVX_UNEXPECTED_END_OF_DATA: Timeout when waiting for HTTP res... Show MoreAfter loading for a while, Qlik REST connector fails with the following error messages:
- QVX_UNEXPECTED_END_OF_DATA: Timeout when waiting for HTTP response from server
- QVX_UNEXPECTED_END_OF_DATA: Failed to receive complete HTTP response from server
This happens even when Timeout parameter of the REST connector is already set to a high value (longer than the actual timeout)
Environment
Qlik Sense Enterprise on Windows
Timeout parameter in Qlik REST connector is for the connection establishment, i.e connection statement will fail if the connection request takes longer than the timeout value set. This is documented in the product help site at https://help.qlik.com/en-US/connectors/Subsystems/REST_connector_help/Content/Connectors_REST/Create-REST-connection/Create-REST-connection.htm
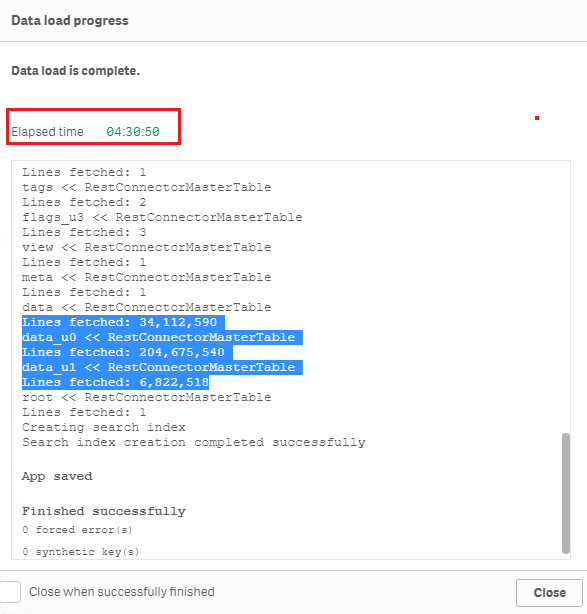
When connection establishment is done, Qlik REST connector does not have any time limit for the actual data load. For example, below is a test of loading the sample dataset "Crimes - 2001 to present" (245 million rows, ~5GB on disk) from https://catalog.data.gov/dataset?res_format=JSON. Reload finished successfully with default REST connector configuration:Therefore, errors like QVX_UNEXPECTED_END_OF_DATA: Timeout when waiting for HTTP response from server and QVX_UNEXPECTED_END_OF_DATA: Failed to receive complete HTTP response from server are most likely triggered by the API source or an element in the network (such as proxy or firewall) rather than Qlik REST connector.
To resolve the issue, please review the API source and network connectivity to see if such timeout is in place. -
Setting Up Knowledge Marts for AI
This Techspert Talks session addresses: Synchronizing data in real time Connecting to Structured and Unstructured data Demonstration of chatbot appl... Show More -
First time access to the Qlik Customer Support Portal fails with: Unauthorized A...
Accessing the Qlik Customer Support Portal for the first time may fail with the error: Unauthorized access. Please try signing out and sign in again. ... Show MoreAccessing the Qlik Customer Support Portal for the first time may fail with the error:
Unauthorized access. Please try signing out and sign in again.
Resolution
This error typically means the required Community profile was not yet completed.
To resolve it:
- Go to Qlik Community
- Log in
- Complete the Profile setup by choosing a Username
- Click Submit
-
Critical Security fix for the Qlik Talend JobServer and Talend Runtime (CVE-2026...
Executive Summary A critical security issue in the Talend JobServer and Talend Runtime has been identified. This issue was resolved in later patches, ... Show MoreExecutive Summary
A critical security issue in the Talend JobServer and Talend Runtime has been identified. This issue was resolved in later patches, which are already available. If the vulnerability is successfully exploited, an attacker could gain full remote code execution on the Talend JobServer and Talend Runtime servers.
This issue was discovered by Harpreet Singh (@TheCyb3rAlphaProfession), Security Researcher.
Affected Software
- All versions of Talend JobServer before TPS-6017 (8.0) or TPS-6018 (7.3).
- All versions of Talend Runtime before 8.0.1.R2026-01-RT or 7.3.1-R2026-01
Severity Rating
Using the CVSS V3.1 scoring system (https://nvd.nist.gov/vuln-metrics/cvss), this issue is rated CRITICAL.
Vulnerability Details
CVE-2026-XXXX – A CVE is pending.
Severity: CVSS:3.1/AV:N/AC:L/PR:N/UI:N/S:U/C:H/I:H/A:H (9.8 Critical)
A critical vulnerability has been found in the Talend JobServer and Talend Runtime that allows unauthenticated remote code execution
The attack vector for this vulnerability is the JMX monitoring port of the Talend JobServer. The vulnerability can be mitigated for the Talend Jobserver by requiring TLS client authentication for the monitoring port. However, the patch will need to be applied to fully mitigate the vulnerability.
For Talend Runtime, the vulnerability can be mitigated by disabling the JobServer JMX monitoring port, which is disabled by default from the 8.0 R2024-07-RT patch.Resolution
Recommendation
Upgrade at the earliest. The following table lists the patch versions addressing the vulnerability (CVE-2026-pending).
Always update to the latest version. Before you upgrade, check if a more recent release is available.
Product Patch Release Date Talend JobServer 8.0 TPS-6017 January 16, 2026 Talend Jobserver 7.3 TPS-6018 January 16, 2026 Talend Runtime 8.0 8.0.1.R2026-01-RT January 24, 2026 Talend Runtime 7.3 7.3.1-R2026-01 January 24, 2026 -
Stream are not visible or available on the hub in Qlik Sense May 2022
After upgrading or installing Qlik Sense Enterprise on Windows May 2022, users may not see all of their streams. The streams appear only after an inte... Show MoreAfter upgrading or installing Qlik Sense Enterprise on Windows May 2022, users may not see all of their streams.
The streams appear only after an interaction or a click anywhere on the Hub.
This is caused by defect QB-10693, resolved in May 2022 Patch 4.
Environment
Qlik Sense Enterprise on Windows May 2022
Workaround
To work around the issue without a patch:
- Locate and open the file: C:\Program Files\Qlik\Sense\CapabilityService\capabilities.json
- Modify the following line:
{"contentHash":"2ae4a99c9f17ab76e1eeb27bc4211874","originalClassName":"FeatureToggle","flag":"HUB_HIDE_EMPTY_STREAMS","enabled":true}
Set it from true to false:
{"contentHash":"2ae4a99c9f17ab76e1eeb27bc4211874","originalClassName":"FeatureToggle","flag":"HUB_HIDE_EMPTY_STREAMS","enabled":false} - Save the file.
If you have a multi node, these changes need to be applied on all nodes.
Note 2: As these are changes to a configuration file, they will be reverted to default when upgrading. The changes will need to be redone after patching or upgrading Qlik Sense. - Restart the Qlik Sense Dispatcher service AND the Qlik Sense Proxy Service
Note: If you have a multi node, all nodes need to be restarted.
Fix
A fix is available in May 2022, patch 4.
Streams will show up (after a few seconds) without the need to click or interact with the hub.
Important NOTE about feature HUB_HIDE_EMPTY_STREAMS:
When you activate HUB_HIDE_EMPTY_STREAMS, you will have an expected delay before all streams appear.
To improve this delay, from Patch 4, you can add HUB_OPTIMIZED_SEARCH (needs to be added manually as a new flag). As of now, HUB_OPTIMIZED_SEARCH tag will be available in the upcoming August 2022 release and is not planned for any patches (yet)
If this delay (seconds) is not acceptable, you will need to disable this HUB_HIDE_EMPTY_STREAMS capability.Cause
This defect was introduced by a new capability service.
Internal Investigation ID(s)
QB-10693
- Locate and open the file: C:\Program Files\Qlik\Sense\CapabilityService\capabilities.json
-
Configure Qlik Sense Mobile for iOS and Android
The Qlik Sense Mobile app allows you to securely connect to your Qlik Sense Enterprise deployment from your supported mobile device. This is the proce... Show MoreThe Qlik Sense Mobile app allows you to securely connect to your Qlik Sense Enterprise deployment from your supported mobile device. This is the process of configuring Qlik Sense to function with the mobile app on iPad / iPhone.
This article applies to the Qlik Sense Mobile app used with Qlik Sense Enterprise on Windows. For information regarding the Qlik Cloud Mobile app, see Setting up Qlik Sense Mobile SaaS.
Content:
- Pre-requirements (Client-side)
- Configuration (Server-side)
- Update the Host White List in the proxy
- Configuration (Client side)
Pre-requirements (Client-side)
See the requirements for your mobile app version on the official Qlik Online Help > Planning your Qlik Sense Enterprise deployment > System requirements for Qlik Sense Enterprise > Qlik Sense Mobile app
Configuration (Server-side)
Acquire a signed and trusted Certificate.
Out of the box, Qlik Sense is installed with HTTPS enabled on the hub and HTTP disabled. Due to iOS specific certificate requirements, a signed and trusted certificate is required when connecting from an iOS device. If using HTTPS, make sure to use a certificate issued by an Apple-approved Certification Authority.
Also check Qlik Sense Mobile on iOS: cannot open apps on the HUB for issues related to Qlik Sense Mobile on iOS and certificates.
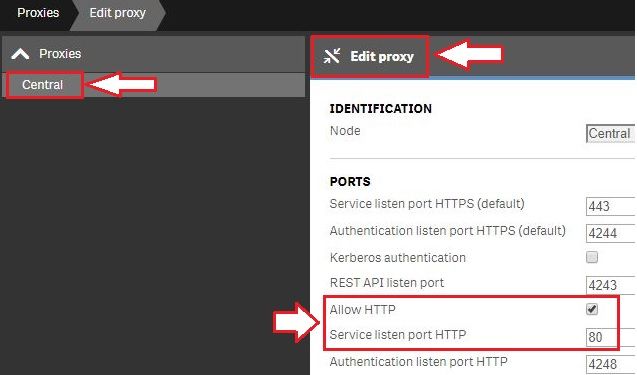
For testing purposes, it is possible to enable port 80.(Optional) Enable HTTP (port 80).
- Open the Qlik Sense Management Console and navigate to Proxies.
- Select the Proxy you wish to use and click Edit Proxy.
- Check Allow HTTP
Update the Host White List in the proxy
If not already done, add an address to the White List:
- In Qlik Management Console, go to CONFIGURE SYSTEM -> Virtual Proxies
- Select the proxy and click Edit
- Select Advanced in Properties list on the right pane
- Scroll to Advanced section in the middle pane
- Locate "Allow list"
- Click "Add new value" and add the addresses being used when connecting to the Qlik Sense Hub from a client. See How to configure the WebSocket origin allow list and best practices for details.
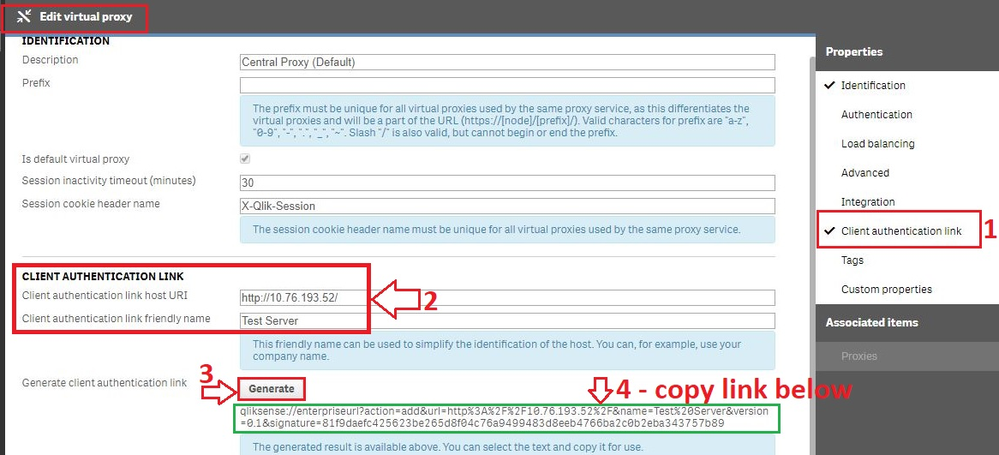
Generate the authentication link:
An authentication link is required for the Qlik Sense Mobile App.
- Navigate to Virtual Proxies in the Qlik Sense Management Console and edit the proxy used for mobile App access
- Enable the Client authentication link menu in the far right menu.
- Generate the link.
NOTE: In the client authentication link host URI, you may need to remove the "/" from the end of the URL, such as http://10.76.193.52/ would be http://10.76.193.52
Associate User access pass
Users connecting to Qlik Sense Enterprise need a valid license available. See the Qlik Sense Online Help for more information on how to assign available access types.
Qlik Sense Enterprise on Windows > Administer Qlik Sense Enterprise on Windows > Managing a Qlik Sense Enterprise on Windows site > Managing QMC resource > Managing licenses- Managing professional access
- Managing analyzer access
- Managing user access
- Creating login access rules
Configuration (Client side)
- Install Qlik Sense mobile app from AppStore.
- Provide authentication link generated in QMC
- Open the link from your device (this can be also done by going to the Hub, clicking on the menu icon at the top right and selecting "Client Authentication"), the installed application will be triggered automatically, and the configuration parameters will be applied.
- Enter user credentials for QS server
-
Qlik Talend Data Integration: tDBConnection adaption for MSSQL Availability Grou...
When setting up a Microsoft SQL Server Always On Availability Group (AG) along with a Windows Failover Cluster, are there any additional SQL Server–si... Show MoreWhen setting up a Microsoft SQL Server Always On Availability Group (AG) along with a Windows Failover Cluster, are there any additional SQL Server–side configurations or Talend-specific database settings required to run Talend Job against a MSSQL Always On database?
Answer
Talend Job need be adapted at the JDBC connection level to ensure proper failover handling and connection resiliency, by setting relevant parameters in the Additional JDBC Parameters field.
Talend JDBC Configuration Requirement
Talend should connect to SQL Server using either the Availability Group Listener (AG Listener) DNS name or the Failover Cluster Instance (FCI) virtual network name, and include specific JDBC connection parameters.
Sample JDBC Connection URL:
jdbc:sqlserver://<AG_Listener_DNS_Name>:1433; databaseName=<Database_Name>; multiSubnetFailover=true; loginTimeout=60Replace and with your actual values. Unless otherwise configured, Port 1433 is the default SQL Server port.
Key Parameter Explanations
multiSubnetFailover=true
Enables fast reconnection after AG failover and is mandatory for multi-subnet or DR-enabled AG environments.
applicationIntent=ReadWrite (optional, usage-dependent)
Ensures write operations are always routed to the primary replica.
Valid values:
ReadWrite
ReadOnly
loginTimeout=60
Prevents premature Talend Job failures during transient failover or brief network interruptions.Best Practice Recommendation
Before promoting any changes to the Production environment, it is essential to perform failover and reconnection stress tests in the DEV/QA environment. This will help to validate the behavior of Talend Job during:
- AG role switchovers
- Network interruptions
- Planned and unplanned failover scenarios
Related Content
Talend JDBC connection parameters | Qlik Talend Help Center
Microsoft JDBC driver support for Always On / HA-DR | learn.microsoft.com
SQL Server JDBC connection properties | learn.microsoft.com
Environment
-
Qlik Talend Administration Center Software Update page shows error: Unexpected H...
Navigating to the Software Update page of the Qlik Talend Administration Center UI leads to the following error: Unexpected HTTP status 302' when acce... Show MoreNavigating to the Software Update page of the Qlik Talend Administration Center UI leads to the following error:
Unexpected HTTP status 302' when accessing (https://talend-update.talend.com/nexus/service/local/status) redirect to (https://talend-update.talend.com/)").
This can affect any Patch Release of Qlik Talend Administration Center (TAC).
SoftwareUpdate
The Configuration page will reflect the error:
Resolution
To resolve, change the Talend update URL (https://talend-update.talend.com/nexus) to https://talend-update.talend.com, removing /nexus from the path.
This is done in the Configuration page.
UpdateURLwithoutNexus
Cause
This issue began to appear after January 26th, 2026, at which point the URL backend was updated.
The URL needs to be changed in the Qlik Talend Administration Center backend.
Environment